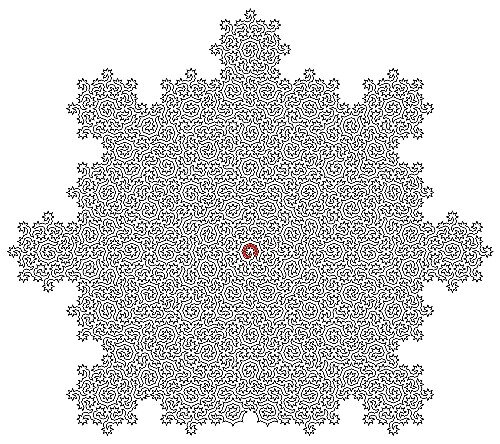
Image shows a Hamiltonian cycle (visited atoms not shown). Credit: University of Bristol
In new research, physicists have harnessed the power of chess to design a series of intricate mazes that could eventually be used to tackle some of the world’s most pressing challenges.
Their unique labyrinthine creations, inspired by the knight’s moves on a chessboard, could help unravel other notoriously difficult problems, including simplifying industrial processes from carbon capture to fertilizer production. The study has been accepted for publication by Physical assessment X and is placed on the arXiv preprint server.
Lead author Dr Felix Flicker, a senior lecturer in physics at the University of Bristol, said: “When we looked at the shapes of the lines we constructed, we saw that they formed incredibly complex mazes. The sizes of the subsequent mazes grow exponentially – and there are infinitely many of them.”
In a knight’s round, the chess piece (which jumps two squares forward and one to the right) visits each square of the chessboard only once before returning to the starting square. This is an example of a “Hamiltonian cycle”: a loop through a map that visits all the stopping points only once.
Theoretical physicists, led by the University of Bristol, constructed an infinite number of increasingly large Hamiltonian cycles in irregular structures describing exotic matter known as quasicrystals.
The atoms in quasicrystals are arranged differently than those in crystals such as salt or quartz. While the atoms in crystals repeat at regular intervals, like the squares on a chessboard, the atoms of quasicrystals do not.
Instead, they do something much more mysterious: quasicrystals can be described mathematically as slices of crystal that live in six dimensions, as opposed to the three dimensions of our known universe.
Only three natural quasicrystals have been found, all in the same Siberian meteorite. The first artificial quasicrystal was created accidentally in the 1945 Trinity Test, the atomic bomb explosion dramatized in the Oppenheimer film.
The group’s Hamiltonian cycles visit every atom on the surface of certain quasicrystals exactly once. The resulting paths form uniquely complex mazes, described by mathematical objects called “fractals.”
These paths have the special property that an atomically sharp pencil can draw straight lines connecting all adjacent atoms without the pencil lifting or the line crossing itself. This has applications in a process known as scanning tunneling microscopy, where the pencil is an atomically sharp microscope tip capable of imaging individual atoms.
The Hamiltonian cycles provide the fastest possible routes for the microscope to follow. This is useful, as it can take a month to produce a state-of-the-art scanning tunneling microscopy image.
The problem of finding Hamiltonian cycles in general situations is so difficult that its solution would automatically solve many important problems that have yet to be solved in mathematics.
Dr Flicker added: “We show that certain quasicrystals represent a special case in which the problem is unexpectedly simple. In this setting, we therefore make a number of seemingly impossible problems tractable. This could include practical purposes spanning several areas of science.”
For example, adsorption is an important industrial process in which molecules attach to the surfaces of crystals. So far, only crystals have been used for adsorption on an industrial scale. If the atoms of a surface allow a Hamiltonian cycle, flexible molecules of the right size can pack themselves with perfect efficiency by lying along these atomic mazes.
The research results show that quasicrystals can be very efficient adsorbers. One application of adsorption is carbon capture and storage, where CO2 Molecules are stopped from entering the atmosphere.
Co-author Shobhna Singh, a PhD researcher in physics at Cardiff University, said: “Our work also shows that quasicrystals could be better than crystals for some adsorption applications. For example, flexible molecules will find more ways to land on the irregularly arranged atoms of quasicrystals. Quasicrystals are also brittle, meaning they easily break up into small grains. This maximises their surface area for adsorption.”
Efficient adsorption could also make quasicrystals surprising candidates for catalysts, which increase industrial efficiency by lowering the energy of chemical reactions. For example, adsorption is a key step in the Haber catalysis process, which is used to produce ammonia fertilizer for agriculture.
More information:
Shobhna Singh et al, Hamiltonian cycles on Ammann-Beenker tilings, arXiv (2023). DOI file: 10.48550/arxiv.2302.01940
Provided by the University of Bristol
Quote: Scientists create world’s most amazingly difficult maze with future potential to boost carbon capture (2024, July 2) Retrieved July 3, 2024, from https://phys.org/news/2024-07-scientists-world-amazingly-difficult-maze.html
This document is subject to copyright. Except for fair dealing for private study or research, no part may be reproduced without written permission. The contents are supplied for information purposes only.