Daedalus could have learned a thing or two from a team of physicists in the UK and Switzerland.
They drew on principles of fractal geometry and strategic chess to create what they call the most difficult maze ever.
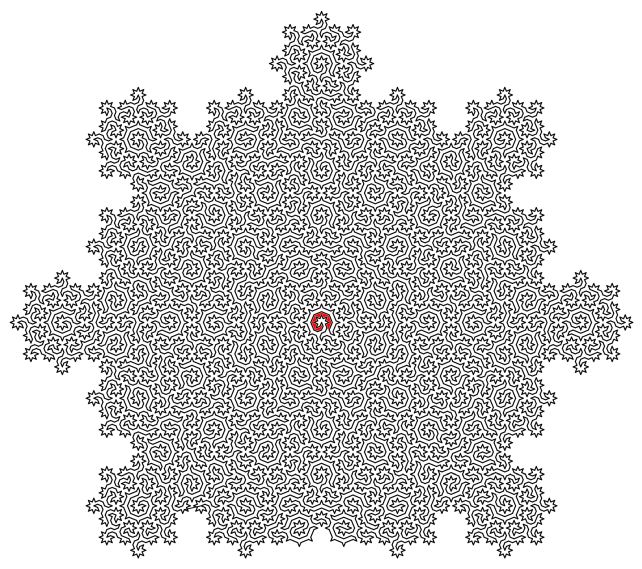
Led by physicist Felix Flicker of the University of Bristol in the United Kingdom, the group has generated routes called Hamiltonian cycles in patterns known as Ammann-Beenker tilings, creating complex fractal mazes that they say describe an exotic form of matter known as quasicrystals.
It was all inspired by the movement of a knight on a chessboard.
“When we looked at the shapes of the lines we constructed, we saw that they formed incredibly complex mazes. The sizes of the subsequent mazes grow exponentially – and there are infinitely many of them,” Flicker explains.
“In a Knight’s tour, the chess piece (which jumps two squares forward and one to the right) visits each square of the chessboard only once before returning to the starting square. This is an example of a ‘Hamiltonian cycle’ – a loop through a map that visits all the stopping points only once.”
Quasicrystals are a form of matter that occurs only very rarely in nature. They are a kind of strange hybrid of ordered and disordered crystals in solids.
In an ordered crystal—salt, or diamonds, or quartz—the atoms are arranged in a very neat pattern that repeats in three dimensions. You can take one part of this lattice and lay it over another, and they will match perfectly.
A disordered or amorphous solid is a solid in which the atoms are all crooked. This includes glass and some forms of ice that are not normally found on Earth.
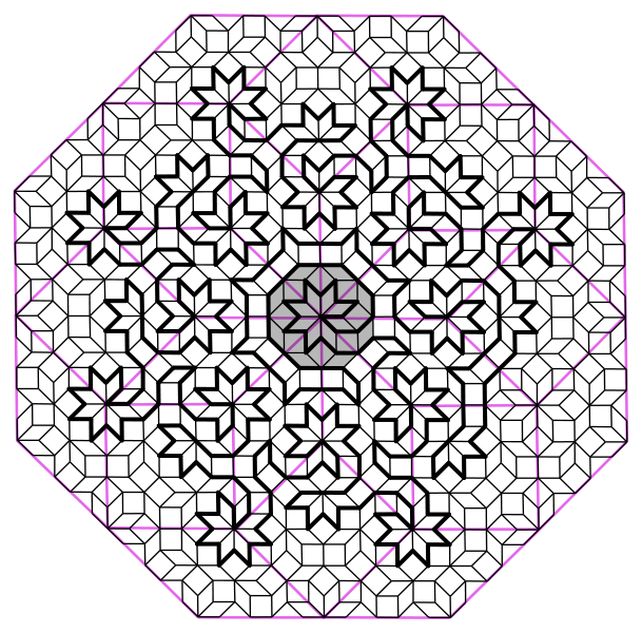
A quasicrystal is a material in which the atoms form a pattern, but the pattern does not repeat perfectly. It may seem quite self-similar, but overlapping parts of the pattern will not match.
These patterns are similar but not identical. They are very similar to a mathematical concept called aperiodic tiling, which involves patterns of shapes that do not repeat in an identical manner.
The famous Penrose tiles are one of them. The Ammann-Beenker tiles are another.
Using a series of two-dimensional Ammann-Beenker tilings, Flicker and his colleagues, physicists Shobhna Singh of Cardiff University in the United Kingdom and Jerome Lloyd of the University of Geneva in Switzerland, generated Hamiltonian cycles that they say describe the atomic pattern of a quasicrystal.
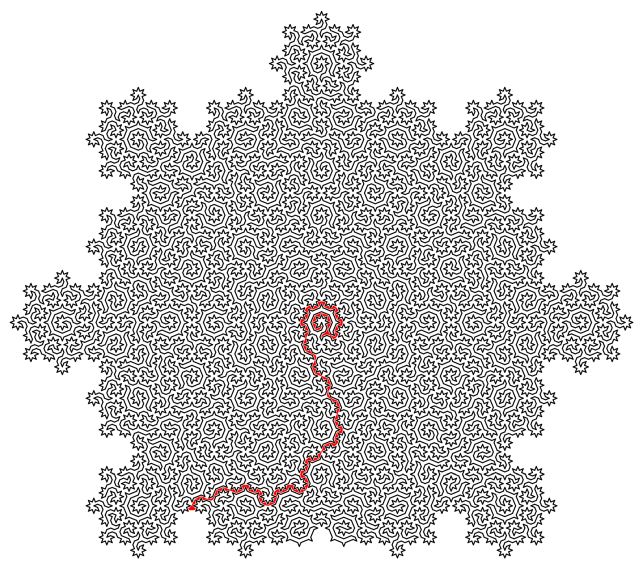
Their generated cycles visit each atom in the quasicrystal just once, connecting all the atoms in a single line that never crosses itself, but continues neatly from beginning to end. And this can be scaled infinitely, generating a kind of mathematical pattern known as a fractal, in which the smallest parts resemble the largest.
This line then naturally produces a maze, with a starting point and an exit. But the research has much larger implications than entertaining restless children in restaurants.
First, finding Hamiltonian cycles is extremely difficult. A solution that would allow Hamiltonians to be identified has the potential to solve many other difficult mathematical problems, from complex pathfinding systems to protein folding.
And, interestingly, there are implications for carbon capture via adsorption, an industrial process that sucks up molecules in a liquid by sticking them to crystals. If we could use quasicrystals for this process instead, flexible molecules could pack themselves together more tightly by lying along the Hamiltonian cycle.
“Our work also shows that quasicrystals may be better than crystals for some adsorption applications,” Singh said.
“For example, bendy molecules will find more ways to land on the irregularly arranged atoms of quasicrystals. Quasicrystals are also brittle, meaning they easily break apart into small grains. This maximizes their adsorption surface.”
And if you happen to have a minotaur that you want to hide somewhere, we know someone who can help you.
The research was published in Physical assessment X.
