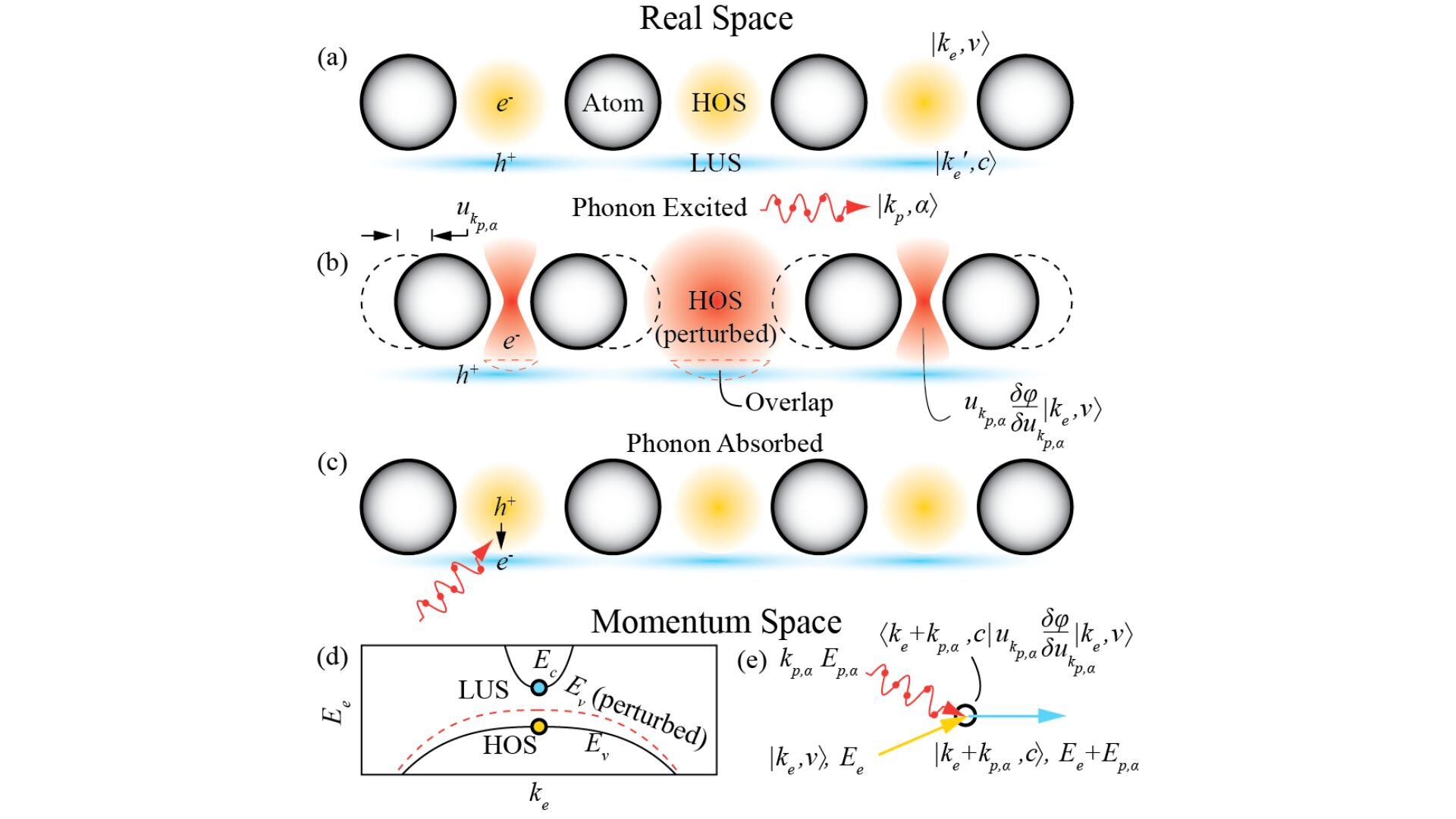
An illustration of electron-phonon coupling between valence and conduction states in momentum and real space. Credit: Cmelni/Wikimedia Commons. commons.wikimedia.org/wiki/File:Electron_Phonon_Coupling_Between_Valence_and_Conduction_States.png.
× close to
An illustration of electron-phonon coupling between valence and conduction states in momentum and real space. Credit: Cmelni/Wikimedia Commons. commons.wikimedia.org/wiki/File:Electron_Phonon_Coupling_Between_Valence_and_Conduction_States.png.
A new study published in Natural physics introduces a theory of electron-phonon coupling that is influenced by the quantum geometry of the electronic wave functions.
The movement of electrons in a lattice and their interactions with the lattice vibrations (or phonons) play a crucial role in phenomena such as superconductivity (resistance-free conductivity).
Electron-phonon coupling (EPC) is the interaction between free electrons and phonons, quasiparticles that represent the vibrations of a crystal lattice. EPC leads to the formation of Cooper pairs (electron pairs), responsible for superconductivity in certain materials.
The new study explores the realm of quantum geometry in materials and how they can contribute to the power of EPC.
Phys.org spoke with the study’s first author, Dr. Jiabin Yu, Moore Postdoctoral Fellow at Princeton University.
Speaking about the motivation behind the study, Dr. Yu: “My motivation is to go beyond common wisdom and find out how the geometric and topological properties of wave functions influence interactions in quantum materials. In this work we focus on EPC, one of the most important interactions in quantum materials.”
Electronic wave functions and EPC
A quantum state is described by a wave function, a mathematical equation that contains all information about the state. An electronic wave function is basically a way to measure the probability of where the electron is in the lattice (arrangement of atoms in a material).
“In condensed matter physics, people have long used energy to study the behavior of materials. In recent decades, a paradigm shift has led us to understand that the geometric and topological properties of wave functions are crucial for understanding and classifying realistic quantum materials .” explained Dr. Yu out.
In the context of EPC, the interaction between the two depends on the location of the electron in the crystal lattice. This means that the electronic wave function determines to some extent which electrons can couple with phonons and influence the conductivity properties of that material.
The researchers in this study wanted to investigate the effect of quantum geometry on the EPC in materials.
Quantum geometry
A wave function, as mentioned earlier, describes the state of a quantum particle or system.
These wave functions are not always static, and their shape, structure, and distribution can evolve over space and time, much like how a wave changes in the ocean. But unlike waves in the ocean, quantum mechanical wave functions follow the laws of quantum mechanics.
Quantum geometry explores this variation of spatial and temporal characteristics of wave functions.
“The geometric properties of single-particle wave functions are called band geometry or quantum geometry,” explains Dr. Yu out.
In condensed matter physics, the band structure of materials describes the energy levels available to electrons in a crystal lattice. Think of them as steps on a ladder, with energy increasing as you go higher.
Quantum geometry affects band structure by affecting the spatial extent and shape of electron wave functions within the lattice. Simply put, the distribution of electrons affects the energy structure or layout for electrons in a crystal lattice.
The energy levels in a lattice are crucial because they determine important properties such as conductivity. In addition, the band structure will vary from material to material.
Gaussian approximation and hopping
The researchers built their model using Gaussian approximation. This method simplifies complex interactions (such as those between electrons and phonons) by approximating the distribution of variables such as energies as Gaussian (or normal) distributions.
This makes it easier to handle mathematically and draw conclusions about the influence of quantum geometry on EPC.
“The Gaussian approximation is essentially a way to relate electron hopping in real space to the quantum geometry of momentum space,” said Dr. Yu.
Electron hopping is a phenomenon in crystal lattices in which electrons move from one place to another. For effective jumping, the wave functions of electrons at adjacent locations must overlap, allowing electrons to tunnel through the potential barriers between locations.
The researchers found that the overlap was affected by the quantum geometry of the electronic wave function, which affected the jumping.
“The EPC often arises from the change of jumping with respect to the lattice vibrations. So the EPC should obviously be enhanced by strong quantum geometry,” explains Dr. Yu out.
They quantified this by measuring the EPC constant, which indicates the strength of the coupling or interaction, using the Gaussian approximation.
To test their theory, they applied it to two materials, graphene and magnesium diboride (MgB2).
Superconductors and applications
The researchers chose to test their theory on graphene and MgB2 because both materials have superconducting properties, driven by EPC.
They found that the EPC for both materials was strongly influenced by geometric contributions. Specifically, the geometric contributions were measured to be 50% and 90% for graphene and MgB2respectively.
They also discovered the existence of a lower bound on the contributions due to quantum geometry. In simple words, there is a minimal contribution to the EPC constant due to the quantum geometry, and the rest of the contribution comes from the energy of the electrons.
Their work suggests that increasing the superconducting critical temperature, the temperature below which superconductivity is observed, can be achieved by improving the EPC.
Certain superconductors such as MgB2 are phonon mediated, meaning that EPC directly affects their superconducting properties. According to the research, strong quantum geometry implies strong EPC, opening a new route for the search for relatively high-temperature superconductors.
“Even if EPC cannot mediate superconductivity alone, it can help cancel some of the repulsive interaction and help generate superconductivity,” added Dr. Yu to it.
Future work
The theory developed by the researchers has only been tested for certain materials and is therefore not universal. Dr. Yu believes the next step is to generalize this theory so that it becomes applicable to all materials.
This is especially important for developing and understanding different quantum materials (such as topological insulators) that can be affected by quantum geometry.
“Quantum geometry is ubiquitous in quantum materials. Researchers know that it should influence many quantum phenomena, but often lack theories that clearly capture this effect. Our work is a step toward such a general theory, but we are still far from a full understanding of it.” concluded Dr. Yu.
More information:
Jiabin Yu et al., Non-trivial quantum geometry and the power of electron-phonon coupling, Natural physics (2024). DOI: 10.1038/s41567-024-02486-0.
Magazine information:
Natural physics
© 2024 Science X Network