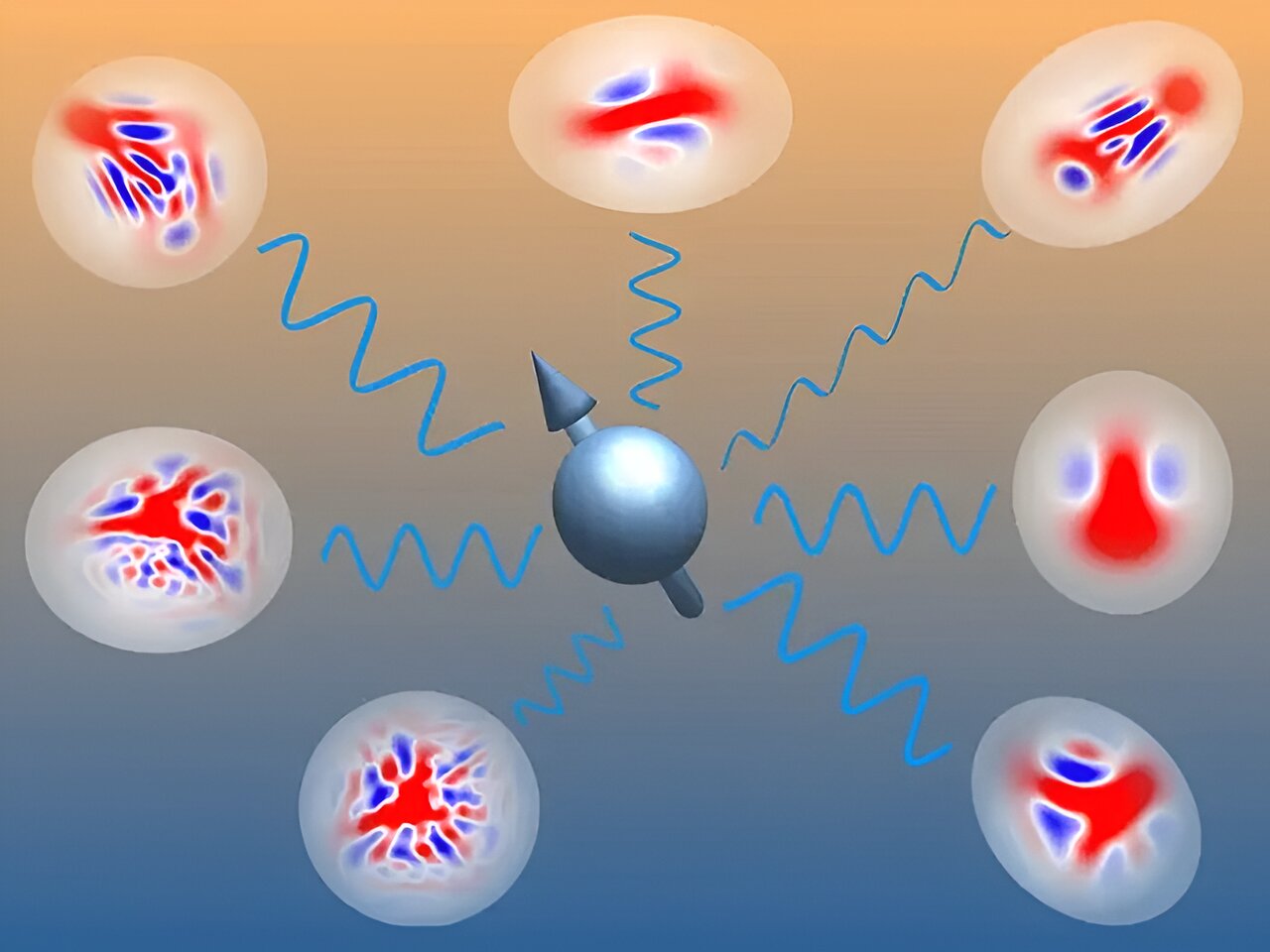
A spin (blue ball with arrow) interacts with the surrounding bosons described by non-Gaussian states – a new computational method to accurately describe what happens in quantum devices. Credit: Jiří Minář
× close to
A spin (blue ball with arrow) interacts with the surrounding bosons described by non-Gaussian states – a new computational method to accurately describe what happens in quantum devices. Credit: Jiří Minář
Many of today’s quantum devices rely on collections of qubits, also called spins. These quantum bits have only two energy levels, the “0” and the “1”. However, spins in real devices also interact with light and vibrations known as bosons, which greatly complicates calculations.
In a new publication in Physical Assessment LettersResearchers in Amsterdam demonstrate a way to describe spin-boson systems and use them to efficiently configure quantum devices into a desired state.
Quantum devices use the idiosyncratic behavior of quantum particles to perform tasks beyond what ‘classical’ machines can do, including quantum computing, simulation, sensing, communications and metrology. These devices can take many forms, such as a collection of superconducting circuits, or a lattice of atoms or ions held in place by lasers or electric fields.
Regardless of their physical realization, quantum devices are typically described in simplified terms as a collection of interacting quantum bits or spins at two levels. However, these spins also interact with other things in their environment, such as light in superconducting circuits or oscillations in the lattice of atoms or ions. Light particles (photons) and vibrational modes of a lattice (phonons) are examples of bosons.
Unlike spins, which have only two possible energy levels (“0” or “1”), the number of levels for each boson is infinite. Consequently, there are very few computational tools for describing spins associated with bosons.
In their new work, physicists Liam Bond, Arghavan Safavi-Naini and Jiří Minář from the University of Amsterdam, QuSoft and Centrum Wiskunde & Informatica work around this limitation by describing systems composed of spins and bosons using so-called non-Gaussian situations. Every non-Gaussian state is a combination (a superposition) of much simpler Gaussian states.
Each blue-red pattern in the image above represents a possible quantum state of the spin-boson system. “A Gaussian state would look like a solid red circle, with no interesting blue-red patterns,” explains Ph.D. candidate Liam Bond. An example of a Gaussian state is laser light, in which all light waves are perfectly synchronized.
“If we take many of these Gaussian states and start to overlap them (so that they are in a superposition), these beautifully complicated patterns emerge. We were particularly excited because these non-Gaussian states allow us to retain many of the powerful mathematical properties. There is a machinery that exists for Gaussian states, while allowing us to describe a much more diverse set of quantum states,” says Bond.
“There are so many possible patterns that classical computers often struggle to calculate and process them. Instead, in this paper we use a method that identifies the most important of these patterns and ignores the others. This allows us to study and design these quantum systems new ways to prepare interesting quantum states.”
The new approach can be leveraged to efficiently prepare quantum states in a way that outperforms other traditionally used protocols. “Fast quantum state preparation can be useful for a wide range of applications, such as quantum simulation or even quantum error correction,” notes Bond.
The researchers also show that they can use non-Gaussian states to prepare ‘critical’ quantum states corresponding to a system undergoing a phase transition. In addition to their fundamental importance, such states can significantly increase the sensitivity of quantum sensors.
Although these results are very encouraging, they are only a first step towards more ambitious goals. So far the method has been demonstrated for a single turn. A natural, but challenging, extension is to include many spins and many bosonic modes at the same time. A parallel direction is intended to account for the effects of the environment that disturbs the spin-boson systems. Both approaches are actively developed.
More information:
Liam J. Bond et al., Fast Quantum State Preparation and Bath Dynamics Using Non-Gaussian Variational Ansatz and Quantum Optimal Control, Physical Assessment Letters (2024). DOI: 10.1103/PhysRevLett.132.170401. On arXiv: DOI: 10.48550/arxiv.2306.01730
Magazine information:
Physical Assessment Letters
arXiv